図1
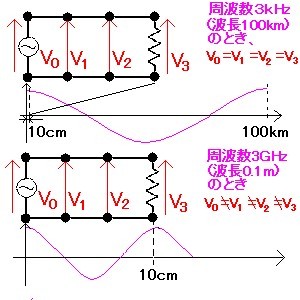
「集中定数」とは、回路網の長さや素子の大きさが、そこを流れる交流の波長に対して無視でき、回路定数や素子定数が1点に集中しているという意味で、集中定数回路とか集中定数素子(コンポーネント)と呼ばれる。これに対して、「分布定数」は、回路網の長さや素子の大きさが波長に対して無視できなく、部品として目に見えない素子が分布していると考える必要がある場合に使用する。例えば、図1の上図のように、信号源と負荷の間の配線の距離が10 cmで、信号源の周波数が3 kHz(波長が100km)とすると、線路のどこで電圧を測定しても同じであるが、図1の下図のように、信号源の周波数が3GHz(波長が10cm)だと、配線(伝送線路)上の位置により電圧が異なるので、なんらかの回路素子(通過する信号の振幅と位相を変化させるもの)が伝送線路上に分布しているものとして考える必要がある。
分布定数回路については、以下のサイトが詳しい。
図1
図2
雑音指数とは、信号がデバイスを通過する際の、デバイスの入力端でのS/N比と出力端でのS/N比との比で、「デバイスを通過することによって生じるS/N比の減少度あるいは劣化度」を意味する。例えば、スペクトラム・アナライザで、増幅器の入力端で図1の(a)のような信号が観測され、出力端で(b)のような信号が観測されたとすると、信号の利得は、-40dBm-(-60dBm)=20dBなので、入力端での雑音パワー(-100dBm)も増幅器によって20dB増幅され、出力端では-80dBmとなるはずだが、実際には、増幅器内部で発生した雑音が加わり-70dBmになっている。この10dBの劣化が雑音指数である。
ここで、雑音指数の定義式を、デバイスの利得をG、デバイス内部で付加される雑音をNとして書き換えると、図2のようにデバイスの入力端での雑音パワーに依存する式となる。入力端での雑音パワーは、kTB（ここで、kはボルツマン定数（1.38×10^－23 J/K）、Tは入力信号源の温度（K）、Bはシステムの雑音帯域幅（Hz））なので、結果として、雑音指数は、入力信号源の温度Tに依存する。IEEEでは、雑音指数を決定するための標準温度Tとして290Kを推奨している。雑音指数の測定法として、Yファクタ法、コールドソース法などがある。
雑音指数についての詳細は、以下のリンクを参照。
無線通信測定に関する翻訳で、bit/s/Hz（ビット/s/Hz）という単位が出てくる。これは、帯域幅1 Hz当たりの情報伝送速度（ビット/s)で、「周波数利用効率」とか「帯域幅効率」とか「スペクトラム効率」と呼ばれている。LTE-Advancedでは、8×8アンテナ構成で30 ビット/s/Hz（ダウンリンク）を目標にしている（参考：LTE-Advancedの概要のp10の表3）。
シャノンの通信路容量の定理（C＝B log（1＋S/N）、C:情報伝送速度（ビット/s）、B：帯域幅（Hz）、S/N：信号対雑音比、参考：情報理論とサンプリングの基礎）から、スペクトラム効率の理論限界C/B（ビット/s/Hz）が決まるが、MIMO（マルチ入力マルチ出力）と呼ばれる受信と送信に複数のアンテナを使用する手法により、スペクトラム効率の理論限界がM・C/B（M：M（送信アンテナの個数）×M（受信アンテナの個数））に向上する。身近な例では、MIMOは無線LANにも使用されている。
無線通信測定（LTE-Advancedなど）に関する翻訳で、Carrier Aggregation（キャリア・アグリゲーション）という言葉が最近よく出てくる。
Carrierとは、無線通信に使用される搬送波のことで、伝送したい情報（音声とかデジタル・データ）をのせて電波で運ぶための信号である。この信号に情報をのせるための操作は変調と呼ばれる（参考：変調のいろいろ～電波に情報をのせる手法の概観～）。Aggregationの動詞aggregateには、「集める、統合する」という意味があり、Carrier Aggregationで「搬送波を集めて統合する」という意味である。
モバイル通信におけるビデオ伝送などの情報伝送量の急激な増加に伴い、情報を伝送するための帯域幅を広くする必要が生じてきた（大量の情報を伝送するためには、搬送波を複雑な変調方式で変調して情報伝送速度を上げる必要があり、占有帯域幅も増加する。参考：通信システムのディジタル変調入門編）。しかし、法律上許可された通信周波数領域のバンド（帯域幅）が狭く、そのバンドを多数のユーザが使用するので、ビデオなどの大量の情報を伝送するための帯域幅が足りなくなる。これを解決するために、同じ許可された通信周波数領域の異なるキャリア（ユーザが使用していないキャリア）を統合したり、異なる許可された通信周波数領域のキャリアを統合して、広い帯域幅を確保する手法を、Carrier Aggregation（キャリア・アグリゲーション）と呼んでいる。
図1
図2
図3
高周波測定に関する翻訳で”impedance matching（インピーダンス整合）”という言葉がよく出てくる。最近では、デジタル回路（PCのマザーボード、CPUダイ内部、ICパッケージ、USB3.0やPCI Expressなどの高速シリアル･ インターフェイス）も高速になり、インピーダンス整合の重要性が増している。このような高周波回路では、インピーダンス整合がとれていないと、信号源の電力の一部が負荷で反射されて、十分な電力を伝えることができない。また、多重反射が発生し（信号源と負荷の間で繰り返し反射が起こり）、アイ・パターンを悪化させる原因となる（参考：ENAオプションTDRを使用した能動デバイスの効果的なホットTDR測定）。
インピーダンス整合とは、信号源と負荷を接続したとき、負荷で消費される電力が最大になるように、接続することである。そのための回路を整合回路という。インピーダンス整合の条件は、負荷側から信号源を見たときのインピーダンスと信号源側から負荷を見たときのインピーダンスが、互いに複素共役になる場合である。したがって、負荷側からの信号源インピーダンスがZs=Rs+jXsであれば、負荷インピーダンスをZl=Rs-jXsにすれば、最大の電力が伝達される。図で、このインピーダンス整合条件を求める。
計測器の翻訳に、jitter（ジッタ）という言葉が出てくる。最近では、AVアンプとかブルーレイ・レコーダにもジッタ低減回路搭載という記述が増えてきている。
ジッタとは、信号波形の時間的なゆらぎである。ジッタが重要な理由は、S/N比が重要な理由と同じである。ジッタが大きいと、アイ・パターンで水平方向にアイが閉じる原因になり、ビット・エラー・レートを悪化させる。これに対して、ノイズが大きいと（S/N比が悪いと）、アイ・パターンで垂直方向にアイが閉じる原因になり、ビット・エラー・レートを増加させる。参考：ディジタル信号の正体を見る。
ジッタについての詳細は、以下のリンクを参照。
計測器の翻訳に、T/s（Transfer per second）という単位が出てくる。例えば、PCI ExpressR rev. 3.0のレシーバ・ストレス・テストで信号を正確に校正することにより、8 GT/sのデータ・レートでの相互運用性を保証がある。
1 T/s（Transfer per second）とは、「１秒間にデータを１個転送する」ことである。データ転送速度にTransfer per secondが使われるのは、バス幅（DIMMモジュールのバス幅が64ビット、グラフィック・カードのメモリ・バス幅が256ビットというように表現される）や1クロック当たりのデータの転送個数（DDRメモリでは2個、DDR2メモリでは4個、DDR3メモリでは8個）などによりデータ転送速度が変わるからである。
例えば、DIMMモジュールのDDR3-1600（PC3-12800）という表記では、1600は1600 MT/s（200 MHz（クロック周波数） × 8（1クロック当たりのデータの転送個数））の意味で、12800は12800 MB/s（1600 MT/s × 64（バス幅） / 8（1バイトは8ビット） ＝12800 MB/s）の意味である。DDR3メモリの動作（クロック）周波数が200 MHzといってもデータ転送速度の指標にならないのである。
計測器の翻訳に、”harmonic”（高調波）という言葉がよく出てくる。これは、非線形デバイス（入力と出力の関係が線形（比例)でないデバイス。理想的なアンプは出力が入力に比例する線形デバイス）に1つの正弦波信号（周波数ω）を入力したときに、出力に現れる周波数がnω（n=2、3、…）の複数の正弦波信号である。楽器や音響工学では倍音と呼ばれる。
図に示すように、入力電圧Vinとして１つの正弦波を非線形デバイスに印加する。このとき、デバイスの非線形性(デバイスの出力電圧Vout)が、Vinのn次多項式で表わされるとする。Voutの式にVin=A1cosωtを代入し、三角関数の公式を使って整理することにより、出力電圧に周波数ωの基本波成分、周波数2ωの2次高調波成分(2次高調波歪み)、周波数3ωの3次高調波成分(3次高調波歪み)、…、周波数nωのn次高調波成分(n次高調波歪み)が現れる。
” total harmonic distortion “（全高調波歪み）という言葉もよく出てくるが、これは、図に示すように、基本波の実効値（RMS）電圧に対する、全ての高調波の実効値電圧の2乗和平方根として定義される。一般的に、高調波成分の振幅は、次数が大きくなると減少する傾向にあるので、全高調波歪みを測定するときには、有限の値の次数を指定する。
計測器の翻訳では、さまざまな単位が出てくる。日本では一部の例外を除き、計量法に準拠してSI単位系で表記する必要があるが、アメリカ合衆国などではヤード・ポンド法で表記されることもあるので、翻訳に際して変換する必要があり厄介である。
SI単位系とはフランス語の”Système International d’Unités”の略称である。国際単位系とも呼ばれる。起源は、国際的に単位を統一しようという目的で1875年にフランスで締結されたメートル条約である。
SI単位には、基本単位と組立単位がある。基本単位には、長さ（メートル、m）、質量（キログラム、kg） 、時間（秒、s）、電流（アンペア、A）、温度（ケルビン、K）、光度（カンデラ、cd）、物質量（モル、mol）の7種類がある。組立単位は、基本単位の乗除だけで表される 。詳細については、以下のリンクを参照。
計測器の翻訳で”uncertainty”という言葉がよく出てくる。例えば、スペクトラム・アナライザの振幅確度の最適化がある。
測定結果の信頼性を表す言葉として測定誤差というのがある。「測定誤差」は、「測定値」－「真の値」で定義され、概念として分かり易いが、「真の値」という不可知の量が定義に含まれているという原理的な困難がある。また、測定結果の信頼性を表す方法が技術分野や国によって異なるという問題もあった。そこで、国際標準化機構(ISO)を中心にして、「計測における不確かさの表現のガイド」（Guide to the Expression of Uncertainty in Measurement、GUM）が出版され、測定結果の信頼性を表す指標として、「不確かさ」（uncertainty）が導入された。そこでは、「不確かさ」は以下のように定義されている。
測定の結果に付随した、合理的に測定量に結びつけられ得る値のばらつきを特徴づけるパラメータ(parameter, associated with the result of a measurement, that characterizes the dispersion of the values that could reasonably be attributed to the measurand)
真の値や誤差という不可知の量を、定義の中で参照することを避けたために、このような回りくどい表現になっている。
不確かさについてのリンクを、以下に挙げておく。
図1
図2
PLLとは、外部からの入力信号(基準信号)と同期した(位相差が等しい)出力信号を生成するための回路で、基本的な回路構成を図1に示す。PLLは、2つの信号間の位相を比較して位相差信号を生成する位相比較器、位相差信号をDC制御電圧に変換するループ・フィルタ(ローパス・フィルタ、積分器)、電圧制御発振器(VCO)で構成される。VCOの出力信号の位相が基準信号より遅れていれば（基準信号が図1のcos(ωRFｔ)、VCOの出力信号が図1のcos(ωRFt－θ)とすると）、位相比較器が位相差信号を生成する。それをループ・フィルタに通すことにより、位相差（図1のθ）の大きさに応じて、VCOの位相を進ませるDC制御電圧（図2の－Bsinθ）が生成され、VCOの出力信号の位相が進む。この動作が、連続的に実行されることにより、VCOの出力信号の位相と基準信号の位相との差がゼロになる(同期される)。PLL自身は、周波数を同期させているのではなく、位相を同期させているが、結果的に周波数も同期させることになる。
図1
図2
時間領域のデータ（波形）を周波数領域のデータ（スペクトラム）に変換することを「フーリエ変換」といい、その逆を逆フーリエ変換という。例えば、時間／周波数／モーダル・ドメインの概要の6ページを読めば、時間領域の波形と周波数領域のスペクトラムは同じデータを別の方向から見ているだけということがわかる。以下で、フーリエ変換と逆フーリエ変換の式を導いておく。
任意の周期関数は、図1のように、その基本波周波数ωとn次高調波周波数nωのsinとcosの無限和で表わすこと(フーリエ級数展開)が可能である。フーリエ級数展開は、オイラーの公式を用いて、複素数表示できる。ここで、基本波周波数ωを0に近づける(周期Tを無限大にする)ことで、周波数領域のスペクトラムを連続化すると、逆フーリエ変換とフーリエ変換の式が得られる。すなわち、周期的に繰り返される時間波形しか扱えないフーリエ級数展開から、周期性のない波形を扱えるフーリエ変換となる。時間領域の連続関数から周波数領域の連続関数に変換することをフーリエ変換といい、その逆を逆フーリエ変換という。
図1
図2
図3
ミキサとは、周波数の高いRF信号(周波数:Frf)を、その周波数に非常に近い周波数(Flo)の局部発振器信号(LO信号)とミックス(混合)することにより、これらの差周波数(Frf－Flo)であるIF(中間周波)信号(この周波数は、低周波なので、回路内で扱いやすくなる)を得るためのデバイスである。このように、高い周波数から低い周波数に変換するプロセスはダウンコンバートと呼ばれる。逆に、IF信号をLO信号とミックスして、RF信号として電波で飛ばすための高周波を得る際にも用いられる。このプロセスはアップコンバートと呼ばれる。別の見方をすると、ミキサは、掛け算回路になっている。すなわち、入力をVrf=Arf・cos(ωrf・t)、Vlo=Alo・cos(ωlo・t)とすると、出力は、Vif=a・Vrf・Vlo=a・Arf・Alo・{cos(ωrf+ωlo)t+cos(ωrf－ωlo)t}となる。このミキサの直後にローパス・フィルタを入れると、差周波数cos(ωrf－ωlo)tを取り出せる。図で、高周波で一般的なダブル・バランスド(2重平衡)ミキサの動作原理を示す。
図1
図2
図3
ある物理量を測定したとき、その測定値に偶然誤差しか含まれていないと仮定する。測定値がz1、z2、…、zn、真の値をｚとすると、偶然誤差は、ξ1=z1-z、ξ2=z2-z、…、ξn=zn-zである。偶然誤差の頻度分布を、全体の頻度が1になるように規格化したものを確率密度関数といい、ξからξ+dξの範囲に誤差が生じる確率は、f(ξ)dξとなる。ξ1、ξ2、…、ξnという偶然誤差が生じる確率P(ξ1、ξ2、・・・、ξn)は、個々の偶然誤差が生じる確率f(ξ1)、f(ξ2)、・・・、f(ξn)が独立な(他の偶然誤差の発生に依存しない)ので、P(ξ1、ξ2、・・・、ξn)=f(ξ1)f(ξ2)・・・f(ξn)=f(z1-z)f(z2-z)・・・f(zn-z)と書ける（図1）。ここで、zが真の値のときにPが最大になる（真の値が測定される確率が最も高い）ので、dP／dz=0である。以下、図2、3のように計算すると、ガウス分布関数(正規分布関数、ガウスの誤差関数)が求まる。
図1、2、3の計算からわかるように、ガウス分布関数は、最初の頻度分布の詳細な形（図1のf(ξ)）には依存せず、個々の偶然誤差が生じる確率が独立で、dlnf(ξ)/dξが解析的(テーラー展開可能)であるという条件のみで決まる。これが自然界にガウス分布が多く存在する理由である。
計測器の翻訳で、サンプリングに関する文章がよく出てくる。計測器もデジタル全盛で、アナログ波形を一定の時間ごとに収集（サンプリングと呼ばれる）してデジタル表示する。このとき、 「aliasing errors（エリアシング誤差）」という言葉に遭遇することがある。
図1
図2
サンプリング・レートとオシロスコープの表示に関する詳細は、以下のリンクが参考になる。
計測器の翻訳に、”intermodulation distortion”という言葉が出てくる。略して、IMDと記されることも多い。これは、非線形デバイス（入力と出力の関係が線形（比例)でないデバイス。理想的なアンプは出力が入力に比例する線形デバイス）に、周波数の近接した複数の正弦波を入力したときにそのデバイスの出力に生じる。
図1
図2
図3
昨日、NHKスペシャルを見ていたら、アメリカの株式売買に占めるブログラム売買の比率が７、８割と言っていたかな。その結果、フラッシュ・クラッシュ（瞬間暴落）が問題になっているとか。そのプログラム売買のプログラムは、機械学習という手法を用いて、過去の膨大な相場データ（今流行のBig Data）からパターンを学習し株価予測を行なっているという。予測が困難な問題に機械学習を用いた例として、将棋のプログラムがある。もう５、６年前になるか、当時のコンピュータ将棋大会で優勝したのがBonanzaという将棋のプログラムだった。他のプログラムが最新鋭のデスクトップPCやクラスタ型PCを用いていたのに対して、Bonanzaが機械学習の結果を利用してノートPCで優勝したのが印象的だった。将棋プログラムも今や機械学習全盛で、プロ・レベルの実力があるという。そのときの将棋における機械学習についてのドキュメントが以下のページの一番下の「おまけ」の「GPW 2006 発表資料」にある。
