計測器の翻訳に、”harmonic”（高調波）という言葉がよく出てくる。これは、非線形デバイス（入力と出力の関係が線形（比例)でないデバイス。理想的なアンプは出力が入力に比例する線形デバイス）に1つの正弦波信号（周波数ω）を入力したときに、出力に現れる周波数がnω（n=2、3、…）の複数の正弦波信号である。楽器や音響工学では倍音と呼ばれる。

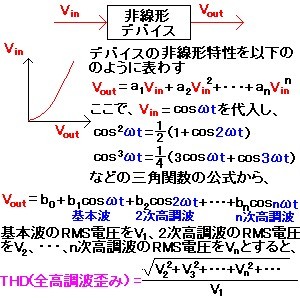
図に示すように、入力電圧Vinとして１つの正弦波を非線形デバイスに印加する。このとき、デバイスの非線形性(デバイスの出力電圧Vout)が、Vinのn次多項式で表わされるとする。Voutの式にVin=A1cosωtを代入し、三角関数の公式を使って整理することにより、出力電圧に周波数ωの基本波成分、周波数2ωの2次高調波成分(2次高調波歪み)、周波数3ωの3次高調波成分(3次高調波歪み)、…、周波数nωのn次高調波成分(n次高調波歪み)が現れる。

” total harmonic distortion “（全高調波歪み）という言葉もよく出てくるが、これは、図に示すように、基本波の実効値（RMS）電圧に対する、全ての高調波の実効値電圧の2乗和平方根として定義される。一般的に、高調波成分の振幅は、次数が大きくなると減少する傾向にあるので、全高調波歪みを測定するときには、有限の値の次数を指定する。