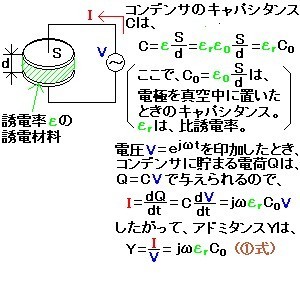
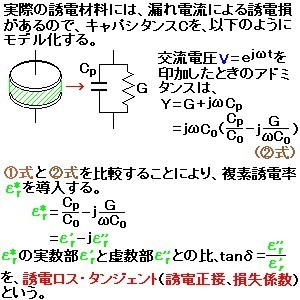
電源測定に関する翻訳で、real power、reactive power、apparent power(有効電力、無効電力、皮相電力)という言葉がよく出てくる(例えば、U1881A/U1882Aパワー測定アプリケーションのp3の表)。
交流(AC)の電力は、交流の瞬時電圧値Vac(t)と瞬時電流値Iac(t)の積である瞬時電力値P(t)=Vac(t)×Iac(t)の、1サイクル(T秒)に渡る時間平均であり、
P=(1/T)∫P(t)dt (1)
で定義される。
交流電圧源Vac(t)=V0cos(ωt)に、負荷として抵抗Rのみが接続されている場合は、オームの法則から、
Iac(t)=Vac(t)/R=(V0/R)cos(ωt)
であり、瞬時電圧値の位相ωtと瞬時電流値の位相ωtが同じ(同相)である。これは、瞬時交流電圧値が正のときは瞬時交流電流値も正であり、瞬時交流電圧値が負のときは瞬時交流電流値も負なので、瞬時電力値は常に正であることを意味し、交流電圧源から供給されたエネルギーが常に負荷で消費されている。このように、負荷で消費される電力を有効電力と呼ぶ。
交流電圧源Vac(t)=V0cos(ωt)に、負荷としてインダクタスLのみが接続されれいる場合は、回路に電流Iac(t)が流れると、電磁誘導の法則、L(dIac(t)/dt)=-V_L(t)からコイルに自己誘導起電力V_L(t)が生じ、キルヒホッフの第2法則からVac(t)+V_L(t)=0が成り立つので、L(dIac(t)/dt)=Vac(t)を積分することにより、
Iac(t)=(1/L)∫V0cos(ωt)dt=(1/ωL)V0sin(ωt)
となり、瞬時電流値の位相は瞬時電圧値の位相ωtに対して90度(π/2)遅れる(sin(ωt)=cos(ωt-π/2))。この場合は、(1)式を計算すると、電力はゼロになる。
同様に、キャパシタンスCのみが接続されている場合は、瞬時電流値の位相が90度進むので(Q=∫I(t)dt=CV(t)の関係を微分)、電力はゼロになる。
どちらの場合も電力がゼロになるのは、供給されたエネルギーが負荷で消費されずに、電源に戻るからである。このように、負荷で消費されずに電源に戻る電力を無効電力と呼ぶ。
一般には、負荷はL、C、Rの合成回路であり、瞬時電圧値Vac(t)と瞬時電流値Iac(t)の位相に差が生じる。この位相差をθとして、Vac(t)=V0cos(ωt)、Iac(t)=I0cos(ωt-θ)を(1)式に代入して電力を計算すると、
P=(1/2)V0×I0×cosθ=Vrms×Irms×cosθ(Vrms、Irmsは、Vac(t)、Iac(t)の実効値)
となる。これは、(電圧ベクトルに対する)電流ベクトルの同相成分Irms×cosθが、実際に負荷で消費されるエネルギーに寄与することを意味し、
有効電力=Vrms×Irms×cosθ [W]、Wは有効電力の単位
となる。
一方、(電圧ベクトルに対する)電流ベクトルの直交成分Irms×sinθは、負荷で消費されず電源に戻るエネルギーに寄与するので、
無効電力=Vrms×Irms×sinθ [var]、varは無効電力の単位
となる。
Vrms×Irms [VA]、VAは皮相電力の単位
は、実際に負荷で消費される電力ではなく、電源から負荷に供給される見かけ上の電力であり、皮相電力と呼ばれる。
また、cosθ=有効電力/皮相電力は力率(power factor)と呼ばれる。
有効電力、無効電力、皮相電力については、以下を参照。
交流電力
電気主任技術者-電験3種の試験と実務の有効電力と無効電力