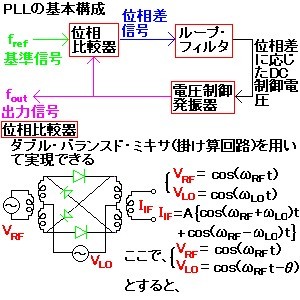
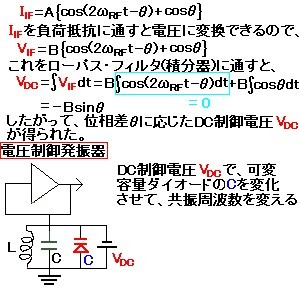
計測器の翻訳で”uncertainty”という言葉がよく出てくる。例えば、スペクトラム・アナライザの振幅確度の最適化がある。
測定結果の信頼性を表す言葉として測定誤差というのがある。「測定誤差」は、「測定値」-「真の値」で定義され、概念として分かり易いが、「真の値」という不可知の量が定義に含まれているという原理的な困難がある。また、測定結果の信頼性を表す方法が技術分野や国によって異なるという問題もあった。そこで、国際標準化機構(ISO)を中心にして、「計測における不確かさの表現のガイド」(Guide to the Expression of Uncertainty in Measurement、GUM)が出版され、測定結果の信頼性を表す指標として、「不確かさ」(uncertainty)が導入された。そこでは、「不確かさ」は以下のように定義されている。
測定の結果に付随した、合理的に測定量に結びつけられ得る値のばらつきを特徴づけるパラメータ(parameter, associated with the result of a measurement, that characterizes the dispersion of the values that could reasonably be attributed to the measurand)
真の値や誤差という不可知の量を、定義の中で参照することを避けたために、このような回りくどい表現になっている。
不確かさについてのリンクを、以下に挙げておく。