信号解析に関する翻訳に、spectrum（スペクトラム）という言葉がよく出てくる（例えば、リアルタイム・スペクトラム・アナライザ（RTSA）Xシリーズ シグナル・アナライザ）。

オシロスコープの画面では、時間経過に対する信号の大きさの変化が（横軸が時間、縦軸が大きさのグラフ上の波形として）表示される。これは、信号の時間領域（タイムドメイン）表示と呼ばれる。スペクトラム・アナライザの画面では、時間領域の信号波形を構成する各周波数成分の大きさ（横軸が周波数、縦軸が大きさのグラフ上に各周波数成分の大きさ）が表示される。これは、信号の周波数領域（周波数ドメイン）表示と呼ばれる。このスペクトラム・アナライザの画面上の各周波数成分の大きさがスペクトラム（スペクトルとも呼ばれる）である（時間／周波数／モーダル・ドメインの概要のp6の図2.1、2.2を参照）。

周波数成分とは、時間領域の信号波形（任意の周期波形）を、その基本波周波数ωとn次高調波周波数nωの正弦波に分解したものである。

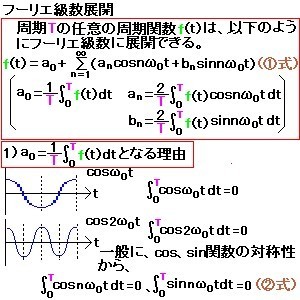
同じ信号の時間領域表示と周波数領域表示（スペクトラム）との関係は、時間領域の任意の周期波形f(t)が、その基本波周波数ωとn次高調波周波数nωの正弦波（sinとcos）の無限和（無限級数）で一意に表わすこと(フーリエ級数展開)が可能であるという事実にもとづいている（左図）。

フーリエ級数展開が可能なことから、フーリエ変換により、時間領域の任意の信号波形を周波数領域のスペクトラムに変換でき、逆フーリエ変換により、周波数領域のスペクトラムから時間領域の波形に変換できる。