高周波測定に関する翻訳で”mixer”という言葉がよく出てくる（例えば、ミキサの変換損失や群遅延を測定するための手法とその比較）。

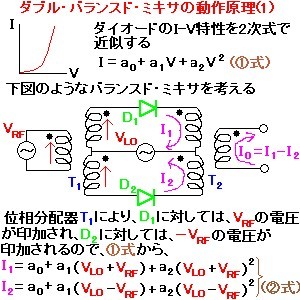
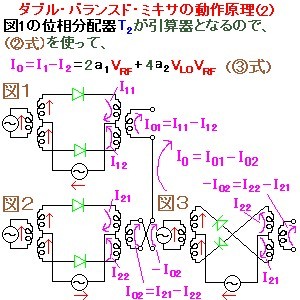
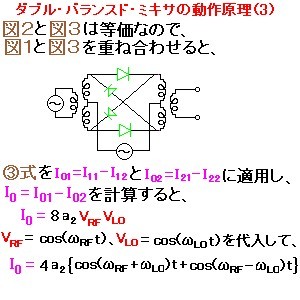
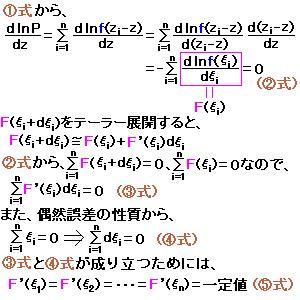ミキサとは、周波数の高いRF信号(周波数:Frf)を、その周波数に非常に近い周波数(Flo)の局部発振器信号(LO信号)とミックス(混合)することにより、これらの差周波数(Frf－Flo)であるIF(中間周波)信号(この周波数は、低周波なので、回路内で扱いやすくなる)を得るためのデバイスである。このように、高い周波数から低い周波数に変換するプロセスはダウンコンバートと呼ばれる。逆に、IF信号をLO信号とミックスして、RF信号として電波で飛ばすための高周波を得る際にも用いられる。このプロセスはアップコンバートと呼ばれる。別の見方をすると、ミキサは、掛け算回路になっている。すなわち、入力をVrf=Arf・cos(ωrf・t)、Vlo=Alo・cos(ωlo・t)とすると、出力は、Vif=a・Vrf・Vlo=a・Arf・Alo・{cos(ωrf+ωlo)t+cos(ωrf－ωlo)t}となる。このミキサの直後にローパス・フィルタを入れると、差周波数cos(ωrf－ωlo)tを取り出せる。図で、高周波で一般的なダブル・バランスド(2重平衡)ミキサの動作原理を示す。

ガウス分布は、正規分布またはガウスの誤差関数と呼ばれ、数学者ガウスが19世紀初頭に測定値の偶然誤差を考察する過程で生まれた。ジッタ測定（例えば、高速データ・レートでのジッタ解析）などで、計測器の翻訳にもよく出てくる。

ある物理量を測定したとき、その測定値に偶然誤差しか含まれていないと仮定する。測定値がz1、z2、…、zn、真の値をｚとすると、偶然誤差は、ξ1=z1-z、ξ2=z2-z、…、ξn=zn-zである。偶然誤差の頻度分布を、全体の頻度が1になるように規格化したものを確率密度関数といい、ξからξ+dξの範囲に誤差が生じる確率は、f(ξ)dξとなる。ξ1、ξ2、…、ξnという偶然誤差が生じる確率P(ξ1、ξ2、・・・、ξn)は、個々の偶然誤差が生じる確率f(ξ1)、f(ξ2)、・・・、f(ξn)が独立な(他の偶然誤差の発生に依存しない)ので、P(ξ1、ξ2、・・・、ξn)=f(ξ1)f(ξ2)・・・f(ξn)=f(z1-z)f(z2-z)・・・f(zn-z)と書ける（図1）。ここで、zが真の値のときにPが最大になる（真の値が測定される確率が最も高い）ので、dP／dz=0である。以下、図2、3のように計算すると、ガウス分布関数(正規分布関数、ガウスの誤差関数)が求まる。

図1、2、3の計算からわかるように、ガウス分布関数は、最初の頻度分布の詳細な形（図1のf(ξ)）には依存せず、個々の偶然誤差が生じる確率が独立で、dlnf(ξ)/dξが解析的(テーラー展開可能)であるという条件のみで決まる。これが自然界にガウス分布が多く存在する理由である。

計測器の翻訳で、サンプリングに関する文章がよく出てくる。計測器もデジタル全盛で、アナログ波形を一定の時間ごとに収集（サンプリングと呼ばれる）してデジタル表示する。このとき、 「aliasing errors（エリアシング誤差）」という言葉に遭遇することがある。

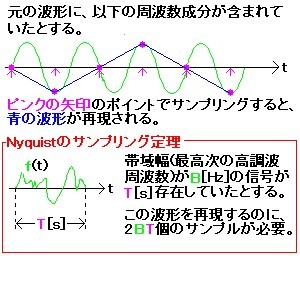
時間領域の波形をある時間間隔(サンプリング間隔またはサンプリング・インターバルと呼ばる。この逆数は、サンプリング周波数と呼ばれる)でサンプリングし、それを再現する際に、元の波形に再現可能周波数(1/2×サンプリング周波数)以上の成分が含まれていると、その周波数成分とサンプリング周波数との差周波数成分(エリアシング誤差、図1の上図)が重畳され、元の波形が歪む。

ナイキストのサンプリング定理によると、エリアシング誤差を避けるには、時間領域の波形に存在する最高周波数成分の2倍以上のサンプリング周波数が必要である。ナイキストのサンプリング定理について、図1、2、3で説明する。

サンプリング・レートとオシロスコープの表示に関する詳細は、以下のリンクが参考になる。

オシロスコープのサンプリング・レートとサンプリング忠実度の評価：正確なデジタル測定の方法