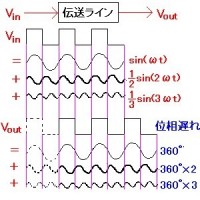
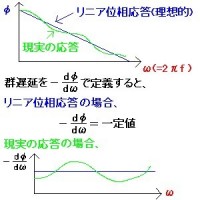
計測器の翻訳に、”intermodulation distortion”という言葉が出てくる。略して、IMDと記されることも多い。これは、非線形デバイス（入力と出力の関係が線形（比例)でないデバイス。理想的なアンプは出力が入力に比例する線形デバイス）に、周波数の近接した複数の正弦波を入力したときにそのデバイスの出力に生じる。

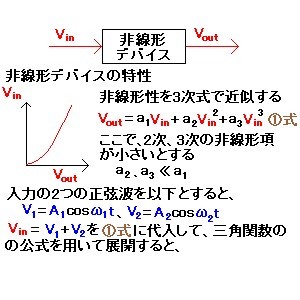
図1に示すような、出力電圧が入力電圧の3次式で表わされるわずかに非線形なデバイスを考える。デバイスの入力に周波数が近接した(ω1≒ω2)2つの正弦波(2トーン信号)を入力すると、三角関数の公式から、図2に示す成分がデバイスの出力に現れる。

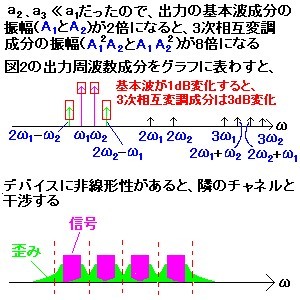
各成分の振幅を周波数軸に対してプロットすると、2つの正弦波の基本波周波数(ω1とω2)に近接した3次の相互変調歪み成分(2ω1-ω2、2ω2-ω1)が現れる（図３）。この3次の相互変調歪み成分の振幅は、その成分の振幅を表わす係数から、2つの基本波成分が1dB変化したとき、3dB変化する。

ここでは、入力信号として2トーン信号を使用して説明したが、一般に、デバイスが非線形であれば、3つ以上の入力トーンに対しても相互変調歪み成分が生じる。例えば、ある周波数帯を細かいチャンネルに分割して多数の通話を行っている携帯電話などでは、その送信機のアンプに非線形性があると、その出力の相互変調歪み成分が隣のチャンネルと干渉したり（隣接チャンネル漏洩電力と呼ばれる）、スペクトラム・リグロース（spectral re-growth）の原因になる。

マイクロ波測定に関する翻訳に、”group delay”という言葉が出てくる。理科系の人でも、「群速度」という言葉は聞いたことがあるが、「群遅延」という言葉ははじめてという人も多いだろう。

これは、波が伝送ラインやフィルタなどのデバイスを通過したときに、その波に生じる歪みの尺度である。例えば、図1のような伝送ラインをパルス波が通過する場合を考える。このとき、通過時間としてちょうどパルス波の1波長に対応する時間がかかるとする。パルス波はその基本波と高調波でsinωt+(1/2)sin2ωt+(1/3)sin3ωt+…と表わされる(フーリエ級数展開される)ので(正しいパルス波のフーリエ級数展開はこうではないが、簡単のためにこうする）、伝送ラインを通過することにより、基本波(周波数ω）は1波長(位相360°)、2次高調波(周波数2ω)は2波長(位相360°×2)、3次高調波(周波数3ω)は3波長(位相360°×3)、…遅れると、元の波形が再現される。すなわち、波が伝送ラインを通過する際に、周波数と位相の遅れ(-φ)が比例するという特性を伝送ラインが持つとき(リニア位相応答という)、歪みが生じることなく元の波形が再現される。現実には、リニア位相応答からのズレが生じる(図2)。このズレを-(dφ／dω)で表わし、伝送時の歪みの尺度として、群遅延と呼んでいる。

最近では、AVアンプに群遅延を補正できるものがある。