伝送ライン測定に関する翻訳に、propagation constant(伝搬定数)という言葉がよく出てくる(例えば、物理層テスト・システム・ソフトウェア(PLTS)2016のp15)。
伝送ラインを分布定数ラインとして扱う、伝送線路方程式(電信方程式)を用いて、伝搬定数を説明する。
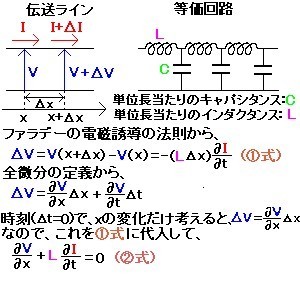
図1のように、伝送ラインを、単位長当たりにキャパシタンスCとインダクタンスLが存在する分布定数素子と考え、位置xでの電流、電圧をI、V、位置x+Δxでの電流、電圧をI+ΔI、V+ΔVとすると、ファラデーの電磁誘導の法則、電荷保存則などより、伝送線路方程式
∂V/∂x+L∂I/∂t=0 (図1の②式)
C∂V/∂t+∂I/∂x=0 (図2の④式)
が得られる。
これらの式から電圧または電流を消去すると、
∂^2V/∂x^2=LC(∂^2V/∂t^2) (図2の⑤式)
∂^2I/∂x^2=LC(∂^2I/∂t^2) (図2の⑥式)
の波動方程式が得られる。電圧に対する方程式(図2の⑤式)と電流に対する方程式(図2の⑥式)がまったく同じになるのは、電磁波が同じ形の電界と磁界の対として伝搬することに対応し、その比(特性インピーダンス)は一定である。
波動方程式の解として、周波数ω、波数k1、初期位相θ1の以下の平面波(正弦波)を考える。
V=V0exp(ωt-k1x+θ1)j
I=I0exp(ωt-k1x+θ1)j、jは虚数単位
このとき、時間微分演算∂/∂tはjωを掛けることに相当するので、上の伝送線路方程式と波動方程式は、
∂V/∂x+jωLI=0
∂I/∂x+jωCV=0
∂^2V/∂x^2=LCω^2V
∂^2I/∂x^2=LCω^2I
となる。
現実には、導体部分を流れる電流によるオーム損(R)と、導体を支えている誘電体部分による誘電損(1/G)があるので(図3参照)、上の伝送線路方程式と波動方程式は、
∂V/∂x+(jωL+R)I=0
∂I/∂x+(jωC+G)V=0
∂^2V/∂x^2=(jωL+R)(jωC+G)V
∂^2I/∂x^2=(jωL+R)(jωC+G)I
となる。
ここで、γ^2=(jωL+R)(jωC+G)=(α+jβ)^2とおくと、波動方程式は、
∂^2V/∂x^2=γ^2V
∂^2I/∂x^2=γ^2I
と書ける。このγを伝搬定数、αを減衰定数、βを位相定数という。この方程式を解くと、αは、電磁波が伝搬方向に進むときの減衰の大きさを表わし、βは、位相変化の大きさを表わすことがわかる。
伝搬定数については、以下を参照