スペクトラム解析に関する翻訳に、window function(窓関数、ウィンドウ関数)という言葉がよく出てくる(例えば、ロングメモリ・オシロスコープのFFT機能を使用したスペクトラム解析のp6)。
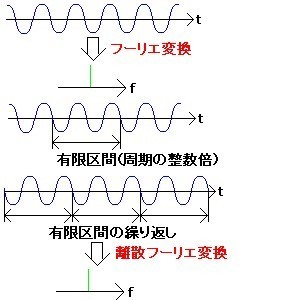
任意の時間領域の信号のフーリエ変換は、その信号を時間に対して-∞から+∞まで積分して求めるが、離散フーリエ変換(FFT)では、積分区間を有限区間で打ち切り、それを離散化する。このため、図1のように、有限区間で打ち切った部分の周期的な繰り返しとして元の信号が表わされる場合は(有限区間で打ち切った部分が周期の整数倍であれば)、フーリエ変換の結果とFFTなどの離散フーリエ変換の結果は一致する。
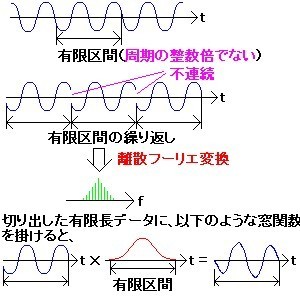
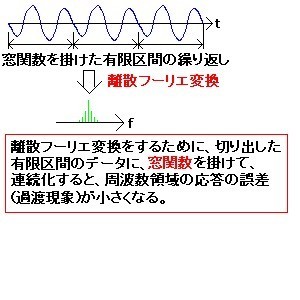
しかし、FFTを行なう場合、データの取り込み区間(有限区間で打ち切きった時間データ)が元の波形の周期の整数倍と正確に一致することはまれである。周期の整数倍と一致しない時間データをFFTすると、その結果である周波数応答に過渡現象(誤差)が生じる。このようにして生じた誤差を「時間窓」による誤差という。この原因は、有限区間で打ち切った時間データの繰り返しとして元の波形を構成すると、有限区間の時間データの最初と最後の継ぎ目の部分で波形が不連続になるからである(図2の上の部分)。この影響を少なくするために、有限区間の時間データに、有限区間以外でゼロとなる関数を掛けて、有限区間で打ち切った時間データの最初と最後の部分がゼロになるようにする(図2の下の部分)。有限区間以外でゼロとなるこのような関数を窓関数と呼ぶ。
窓関数として、ハミング窓、ハニング窓、フラットトップ窓などがある。
窓関数については、以下を参照
(株)小野測器のホームページ > サポート > 小野測器技術レポート > FFTアナライザについての7.FFTと時間窓(ウィンドウ)