増幅器などの非線形デバイスの測定に関する翻訳に、third-order intercept point(3 次インターセプト・ポイント)という言葉がよく出てくる(例えば、PNA-X ネットワーク・アナライザによる正確な相互変調歪み測定のp3)。third-order intercept point(3次インターセプト・ポイント)は、IP3またはTOIと略記されることがある。
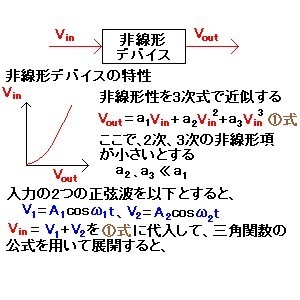
図1に示すような、出力電圧が入力電圧の3次式で表わされる、わずかに非線形なデバイスを考える。デバイスに周波数が近接した(ω1≒ω2)2つの正弦波(2トーン信号)を入力すると、三角関数の公式から、図2に示す成分が出力に現れる。
各成分の振幅を周波数軸に対してプロットすると(図3の上)、2つの正弦波の基本波周波数(ω1とω2)に近接した3次相互変調成分(2ω1-ω2、2ω2-ω1)が現れる。この3次相互変調成分は、(ω1≒ω2から、2ω1-ω2≒ω1≒ω2≒2ω2-ω1なので)信号波(ω1とω2)に非常に近接した妨害波となり、フィルタで除去するが困難である。また、これらの成分の振幅を表わす係数から、2つの基本波成分の振幅が1dB変化したとき、3次相互変調成分の振幅は3dB変化する。
これを両対数グラフ(図3の下)で表わすと、入力振幅に対する、出力の基本波成分の振幅および3次相互変調成分の振幅の関係は比例関係であり、3次相互変調成分の振幅を表す直線(緑色)の傾きは、基本波成分の振幅を表す直線の傾き(ピンク色)の3倍になる。基本波成分と3次相互変調成分はやがて利得圧縮(飽和)により比例関係から外れるが、それぞれの比例部分を延長した2つの直線が交わるポイントが3次インターセプト(TOI)ポイントである。3次インターセプト・ポイントを求めておくと、基本波のみ観測されていて3次相互変調成分がノイズに隠れて見えない場合でも、その大きさを見積もることができる