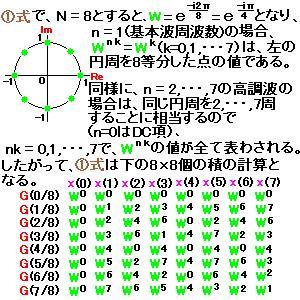
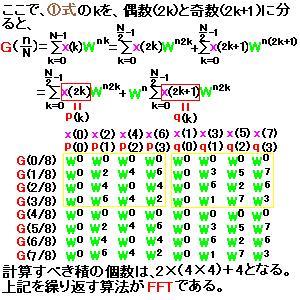
デジタル変調に関する翻訳に、EVMという言葉がよく出てくる（例えば、Agilent MXAシグナル・アナライザ N9073A-1FP W-CDMA測定アプリケーション N9073A-2FP HSDPA/HSUPA測定アプリケーションのp23）。
EVMは、Error Vector Magnitude（エラー・ベクトル振幅） の略で、デジタル変調信号の品質の指標である。
デジタル変調信号は、横軸を搬送波と同じ位相、縦軸を搬送波と直交する位相にとったコンスタレーション図上のシンボル・ポイント（シンボル位置とも呼ばる）で表される。この理想的なシンボル位置と復調器により復調（測定）されたシンボル位置とのずれがエラー・ベクトルで、このエラー・ベクトルの大きさと理想シンボル位置の大きさとの比がエラー・ベクトル振幅（通常％単位で表される）である。
EVM（エラー・ベクトル振幅）については、以下を参照
春に続いて、またまた行ってまいりました。ビールの楽園「けやきひろば秋のビール祭り2013」です。
これまで駅前のけやきひろばでの開催でしたが、今回からお隣のさいたまスーパーアリーナへと引越しです。雨が降るあいにくの空模様となりましたが、さっそくアリーナの利点が活かされることとなりました。
会場が全天候OKになっただけではなく、飲食スペースも拡大し出店ブルワリーもパワーアップしています。もはや、一日で全てを飲み尽くすのは難しいレベルとなりました。場所取りの問題さえ解消できれば（有料の指定席もあります）、大人数で行ったほうが手分けしていろいろと楽しめるかもしれません。
それはさておき、これまでの外飲みの爽快さと比べて室内会場はどんなものかと心配だったのですが、それは全くの杞憂でした。天井は高く、空調もバッチリ。ビールは言うまでもなく、アテもリーズナブルで最高のイベントだったと思います。
それでは、来年の春に会場でお会いしましょう。
信号解析に関する翻訳に、FFTという言葉がよく出てくる（例えば、高速オシロスコープの歪み特性の評価 AgilentとTektronixの比較のp3）。FFTは、Fast Fourier Transform（高速フーリエ変換） の略で、離散フーリエ変換を高速に計算するための算法である。
図1
図2
図3