フィルタ設計ソフトウェアに関する翻訳で、zero（零点）という言葉がよく出てくる（例えば、Genesys S/FilterソフトウェアによるカスタムRF/マイクロ波／アナログフィルターのシンセシスのp3）。

図1.

図2.

図3.

重ね合わせの原理が成り立つ線形システムに正弦波を入力して、その定常応答の出力を解析する場合は、周波数応答関数（伝達関数）H(ω)=Y(ω)/X(ω)[X(ω)：入力信号の各フーリエ成分（フーリエ変換）、Y(ω)：出力信号の各フーリエ成分（フーリエ変換）]を用いる方法が便利である。

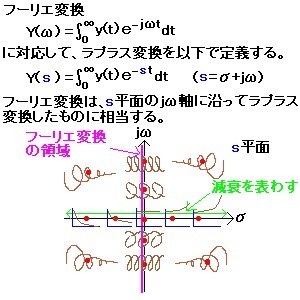
一方、入力波形の急激な変化に対する過渡的な応答を解析する場合は、ラプラス変換の伝達関数を用いる方法が便利である。ラプラス変換では、周波数ωの拡張概念である複素周波数s=σ+jωで減衰項を導入することにより、システムの挙動を過渡状態を含めて考えることができる（図1および図2）。

ラプラス変換の伝達関数は、G(s)=Y(s)/X(s)[X(s)：入力信号のラプラス変換、Y(s)：出力信号のラプラス変換]で定義され、多くの場合、図3のようなsの有理式で表わされる。この有理式の分子を因数分解して、分子がゼロとなるsを、伝達関数が何も伝達しないという意味で零点という。同様に、分母を因数分解して、分母がゼロとなるsを、伝達関数が無限大の量を伝達するという意味で極という（これらの零点や極を複素平面上にうまく配置することにより、所望の伝達特性（伝達関数）を持つフィルタを設計できる）。

ラプラス変換については、以下を参照

The Laplace Transform（英語pdf）

東京工業大学 大学院理工学研究科 電子物理工学専攻 松澤・岡田研究室のホームページ > Lectures > 信号システム解析 > 2006 03