回路シミュレーションに関する翻訳で、convolution(畳み込み)という言葉がよく出てくる(例えば、IBIS AMIチャネル・シミュレーション・フローを用いたSERDESデザインについてのp4)。
回路のインパルス応答を測定するだけで、あらゆる入力信号に対する応答(出力信号)が「畳み込み演算」により求めることができる。

ある系に、入力信号x[t]を印加したときの出力信号y[t]を考える。この系は、線形性(重ね合わせの原理が成り立つ)、時不変性(時刻が異なっても入力と出力の関係が同じ)、因果律を満たす(時刻nにおけるシステムの出力y[n]は、過去の入力x[n]、x[n-1]、…のみに依存)とする。
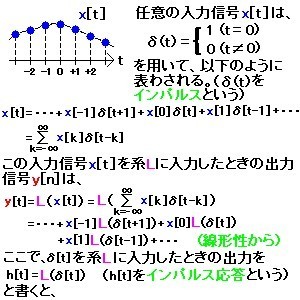
この系に、インパルス関数δ(n)[n=0のときδ(n)=1、n≠0のときδ(n)=0となる関数]を入力したときの出力(インパルス応答関数)をh(n)とすると、y[t]=x[t]h[0]+x[t-1]h[1]+…となる。これを、離散系のたたみ込み演算(コンボリューション)という(図参照)。
このような系では、インパルス関数δ[n]の応答h[n]を測定すれば、上の式から、任意の入力x[t]に対する出力y[t]が得られる。連続系では、上の離散系のたたみ込み演算を連続化して、図のような積分表示となる。
畳み込み演算の簡単な説明については、以下を参照


